FFT based frequency calculation (implementation)

In a previous article I described the goal, which was to do a simple tool to measure the fundamental frequency of a simple sine wave. In this article, I describe the implementation, which is based on 2 open source libraries:

1.  lib FFTW for Fourier calculation
2. libsndfile for wav file parsing

Using those libraries allows a great deal of flexibility in testing various options, samples quantity, FFT types (1 or 2 dimensions). Both libraries quite naturally expose some form of Init functions, Worker functions and cleanup functions.

The following will concentrate on the essential issues for using both libraries and some gotchas but I deliberately  skept all the boiling plate of command line parameter parsing, result formatting, error handling … as this is very standard code.

Some design choices

THD calculation

Interestingly, computing the THD (Total Harmonic Distortion)  was a bit more challenging …. as there are a lot of slightly different definitions for THD. After some research, I landed on this  very comprehensive site    which helped converge to the following definition:

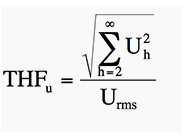
// Definition THDf (aka THD) = SQRT(SUM(RMS(Y(2..N))) / RMS(Y(1)
// Where:
// Y(i) = Amplitude of harmonic i
// Y(1) = Amplitude of harmonic 1 (Fundamental frequency)
// Note: in the litterature, Fundamental is 1, harmonics start at 2

Which basically means the ratio of the energies found in all harmonics but the fundamental, to the energy of the fundamental. Different definitions can be found, but I opted for this one.

Number of FFT POINTS

The design assumption was that the input waveform is given as a .wav format file, made of a few seconds of a 16-bit mono PCM stream. The frequency was 1000 Hz and the stream was sampled at 48 kHz.

1. I want to be able to appreciate a frequency deviation from the nominal 1000 Hz, knowing that the deviation will likely be either significant, or almost zero.
2. Memory consumption of the tool is not very critical, but should still be reasonable. Processing time is more important.

As the number of points together with the sampling frequency will define the  frequency resolution, the more points we take, the more memory we consume but the better our resolution. To stay with reasonable numbers, I opted for 1024 samples. As the sampling was 48 kHz (so Shanon frequency is 24 kHz), this translates to frequency bins of about 48 Hz.This can be improved with an interpolator.

What is an interpolator ?

It basically takes 2 successive samples of a FFT, and computing a weighted middle point, which is assumed to be a more precise frequency result. There are various  methods, linear, quadratic, barycentric, etc .. I opted for the Quinn interpolator

Software architecture

Although I  use of Open Source libraries, I wanted to decorrelate as much as possible the core code from the libraries internals. There is an obvious reason for that. As this tool, would be used in mass production for commercial products, we needed to maintain flexibility to change library components (for example, if any legal issue arises).

In the same vein, two more constraints can be listed

1. We wanted very low reliance on external libraries, so exit Python and the like.
2. The tool will be integrated into a manufacturing line. No User to contemplate the output, but an  automated test and validation system. So the result shall expose very simple numerical values, in an easy to parse format  (TAB delimited, etc ..).

For all those fairly classical reasons, I built small wrappers around the FFT library, the WAV parsing library and the THD calculation routines. This should allow easy maintenance and evolution. The code was built with VC13 (command line executable) in C language.

Implementation

First, we defined three interfaces (poor man API :)) for

libsndfile library

extern int wavLibInit(const char * const);
extern int wavGetAudioSamples(float **buf, unsigned int* count);
extern int wavGetSamplingFrequency(void);
extern void wavLibCleanup();

FFT Library

// Windowing
#define HAS_HANN_WINDOW

double* fftLibInit(int samplesNb, int freq);
fftw_complex *fftLibCompute(void);
int fftLibFindCentralFrequency(fftw_complex* out);
int fftLibGetFreqBin(void);
void fft_window(float *inputBuf, int sampleNb);
void fftLibCleanup(void);

THD Calculation module

typedef enum { THD_FUNDAMENTAL, THD_RELATIVE, THD_NOISE } thd_t;

double thdCompute (const fftw_complex *buf, int size, int f0bin, thd_t type);

This is not perfect, as it still relies on a proprietary type (fftw_complex) which is defined the the FFT library. However, as this a very simple  “double [2]” vector, this is generic enough and not worth the effort of abstracting it (call for debate here ..)

FFTW Library usage

To use the lib, we need to first allocate a buffer for the samples, by using the supplied “fftw-malloc” and passing the number of samples to work on.

(extract from the wrapper fftLibInit method) 

 if (in = (double*)fftw_malloc(sizeof (double)* samplesNb))
 return in;
     return NULL;

Then, we need to allocate a buffer for the output samples (hence the importance of careful choice of the Number Of Samples …. twice the memory is needed.

out = (fftw_complex*)fftw_malloc(sizeof (fftw_complex)* nc);

Then we need to define a “plan”. In  FFTW terminology, this is a set of parameters describing which FFT we want to use (direct, reverse), what type of numbers we operate on, etc …. In our case, we needed a One Dimensional DFT, operated on Real Numbers. Refer to ffttw3 official site  for an exhaustive list of all. There are a lot of them !

plan_forward = fftw_plan_dft_r2c_1d(nc, in, out, FFTW_ESTIMATE);

Then ….. we execute the plan 🙂

fftw_execute(plan_forward);

As a side effect, the output samples are present in the “out” buffer, previously allocated. Once done, we cleanup everything

void fftLibCleanup(void)
{
 fftw_destroy_plan(plan_forward);
 fftw_free(in);
 fftw_free(out);
}

Libsndfile library usage

This lib operates on custom types, which need to be defined beforehand. Here is the code extract

#include <sndfile.h>

#define NB_AUDIO_SAMPLES (1024*1)

static SNDFILE* inputWav, *refWav;
static SF_INFO wavFileInfo;
static float * localBuf;

......
......
 memset(&wavFileInfo, 0, sizeof(wavFileInfo));
 if ((inputWav = sf_open(file_name, SFM_READ, &wavFileInfo)) == NULL)
 return (-EBADF);
return 0;
......

Calling the sf_open will get automatically all the file meta-data into the wavFileInfo structure. From there, sampling rate can be extracted, encoding width, number of channels, etc.

Then, the file is simply read, the WAV format is interpreted and the audio samples are put in the provided buffer. Here is my small wrapper around these operations

int wavGetAudioSamples(float **buf, unsigned int * count)
{
 // Allocate mem to read in the channel data
 int bytesPerSample;
 if ((bytesPerSample = wavGetBytesPerSample(&wavFileInfo) == -EINVAL))
 return (-EINVAL);

*buf = (float *)malloc((size_t)wavFileInfo.frames*wavFileInfo.channels*sizeof(float));

sf_count_t samples = sf_read_float(inputWav, *buf, NB_AUDIO_SAMPLES * wavFileInfo.channels); // read 1000 samples both channels ... but will process only one
 *count = (unsigned int)samples;
 return 0;
}

we use the previously defined xxx structure to retrieve info about size, number of samples (wavFileInfo.frames, wavFileInfo.channels) . Note also the sf_read_float which would do the translation to float as well (As this is need for the FFTW lib).

Then, some cleanup

void wavLibCleanup()
{
 sf_close(inputWav);
 free(localBuf);
}

Results and gotchas

There is an interesting and very important point in the FFTW operations: the results are NOT normalized. This is very well describe in the FFTW documentation . As stated

FFTW computes an unnormalized transform, in that there is no coefficient in front of the summation in the DFT. In other words, applying the forward and then the backward transform will multiply the input by n.

so that mean that you need to take this into account in the calling code. Otherwise the results will look fancy.

One can apply a Windowing function before calling the FTT. I tried various window, ended up applying an Hann window as follows:

static void fft_hann_window(float *inputBuf, int sampleNb)
{
 float multiplier;
 for (int i = 0; i < sampleNb; i++)
 {
 multiplier = 0.5f * (1 - cosf(2.0f * (float)M_PI*i / sampleNb));
 inputBuf[i] *= multiplier;
 }
}

but I couldn’t see a dramatic effect 🙁 and even sometimes, it seemed to me there was a degradation on the frequency calculation. This is FFS (For Further Study)

So when everything was bundled together (and he tool coined “wavcheck”), we got the following:

C:\>wavcheck.exe
wavcheck                 version 1.0.0
simple manufacturing wv file analyser
Usage:
wavecheck [-thd] <sound.wav>

Where:

---> thd : adds the thd calculation
---> <sound.wav> is the .wav file to analyze
C:\>

and the output 🙂

Et voila !

References

1. http://www.ericjacobsen.org/FTinterp.pdf
2. https://dspguru.com/dsp/howtos/how-to-interpolate-fft-peak/
3. FFTW3 library
4. Libsndfile library